Granular materials
Our group’s work on granular materials involves developing predictive continuum models for dense granular flow. Granular materials are mixtures of discrete, macroscopic particles and are ubiquitous in nature as well as in everyday life – in forms such as sand, gravel, pharmaceutical pills, food grains, and industrial powders. However, certain mechanical behaviors of these materials remain challenging to predictively model, including dense flow and size-segregation phenomena. Predictive models are crucial to robust engineering design involving granular media, and the benefits of improved modeling capabilities are numerous.
One aim of our group’s research has been to elucidate the rheology of steady flows of a dense collection of dry, hard particles that are roughly all the same size (monodisperse). The challenge is that local constitutive equations that relate the local stress state to the local state of strain rate at a point cannot capture the phenomenology of dense granular flows, since the deformation of a granular media displays a strong dependence on the size of the constituent grains, and to this end, we pursue nonlocal continuum modeling.
- Shihong Li and David L. Henann. Nonlocal continuum modeling of dense granular flow in a split-bottom cell with a vane-shaped intruder. Physical Review E 102 (2020) 022908.
- Shihong Li and David L. Henann. Material stability and instability in non-local continuum models for dense granular materials. Journal of Fluid Mechanics 871 (2019) 799-830.
- Daren Liu and David L. Henann. Size-dependence of the flow threshold in dense granular materials. Soft Matter 14 (2018) 5294-5305.
- Daren Liu and David L. Henann. Nonlocal continuum modeling of steady, dense granular heap flows. Journal of Fluid Mechanics 831 (2017) 212-227.
 Another aim of our group’s work on dense granular materials relates to modeling size-segregation in dense, bidisperse granular systems, made up of particles of two sizes. Dense granular systems, consisting of particles of disparate sizes, segregate based on size during flow, resulting in complex, coupled segregation and flow patterns. We utilize discrete-element method (DEM) simulations of flow of dense, bidisperse granular systems to inform continuum constitutive equations for the relative flux of large and small particles.
Another aim of our group’s work on dense granular materials relates to modeling size-segregation in dense, bidisperse granular systems, made up of particles of two sizes. Dense granular systems, consisting of particles of disparate sizes, segregate based on size during flow, resulting in complex, coupled segregation and flow patterns. We utilize discrete-element method (DEM) simulations of flow of dense, bidisperse granular systems to inform continuum constitutive equations for the relative flux of large and small particles.
- Daren Liu, Harkirat Singh, and David L. Henann. Coupled continuum modelling of size segregation driven by shear-strain-rate gradients and flow in dense, bidisperse granular media. Journal of Fluid Mechanics 976 (2023) A16.
Constitutive modeling of elastomeric foams (in collaboration with the Franck Lab)
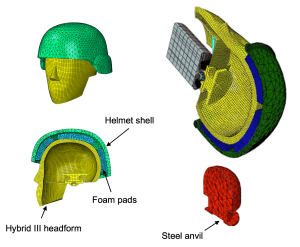 Viscoelastic elastomeric foams are widely used in equipment for impact protection and exhibit mechanical behavior marked by high compressibility and strong coupling between the volumetric and distortional responses. Developing predictive constitutive models for these materials remains challenging despite their ubiquity. Our group’s work seeks to (1) develop and validate constitutive models for elastomeric foam materials, including viscoelastic, poroelastic, and temperature-dependent behavior, and (2) utilize these models to design improved protective equipment, such as helmets.
Viscoelastic elastomeric foams are widely used in equipment for impact protection and exhibit mechanical behavior marked by high compressibility and strong coupling between the volumetric and distortional responses. Developing predictive constitutive models for these materials remains challenging despite their ubiquity. Our group’s work seeks to (1) develop and validate constitutive models for elastomeric foam materials, including viscoelastic, poroelastic, and temperature-dependent behavior, and (2) utilize these models to design improved protective equipment, such as helmets.
- Xiuqi Li, Jialiang Tao, Alexander K. Landauer, Christian Franck, and David L. Henann. Large-deformation constitutive modeling of viscoelastic foams: Application to a closed-cell foam material. Journal of the Mechanics and Physics of Solids 161 (2022) 104807.
- Alexander K. Landauer, Xiuqi Li, Christian Franck, and David L. Henann. Experimental characterization and hyperelastic constitutive modeling of open-cell elastomeric foams. Journal of the Mechanics and Physics of Solids 133 (2019) 103701.
- Alexander K. Landauer, Mohak Patel, David L. Henann, and Christian Franck. A q-factor-based digital image correlation algorithm (qDIC) for resolving finite deformations with degenerate speckle patterns. Experimental Mechanics 58 (2018) 815-830.
Modeling of inertial microcavitation in soft materials (in collaboration with the Franck Lab)
Another research interest in our group relates to inertial microcavitation in soft materials, focusing on the dynamics of small bubbles formed in soft solids that are as compliant as a few kilopascals using either laser- or ultrasound-based methods. The motivation for this work is twofold: (1) inertial microcavitation is a novel route for mechanical characterization of soft materials at high strain-rates (greater than 1000 1/s) – a task which is beyond existing experimental techniques – and (2) inertial microcavitation in brain tissue is a potential mechanism of traumatic brain injury.
- Anastasia Tzoumaka, Jin Yang, Selda Buyukozturk, Christian Franck, and David L. Henann. Modeling high strain-rate microcavitation in soft materials: the role of material behavior in bubble dynamics. Soft Matter 19 (2023) 3895-3909.
- Alexander McGhee, Jin Yang, Elizabeth C. Bremer, Zhiqin Xu, Harry C. Cramer III, Jonathan B. Estrada, David L. Henann, and Christian Franck. High-Speed, Full-Field Deformation Measurements Near Inertial Microcavitation Bubbles Inside Viscoelastic Hydrogels. Experimental Mechanics 63 (2023) 63-78.
- Selda Buyukozturk, Jean-Sebastien Spratt, David L. Henann, Tim Colonius, and Christian Franck. Particle-Assisted Laser-Induced Inertial Cavitation for High Strain-Rate Soft Material Characterization. Experimental Mechanics 62 (2022) 1037-1050.
- Jin Yang, Anastasia Tzoumaka, Kazuya Murakami, Eric Johnsen, David L. Henann, and Christian Franck. Predicting complex nonspherical instability shapes of inertial cavitation bubbles in viscoelastic soft matter. Physical Review E 104 (2021) 045108.
- Jonathan B. Estrada, Carlos Barajas, David L. Henann, Eric Johnsen, and Christian Franck. High strain-rate soft material characterization via inertial cavitation. Journal of the Mechanics and Physics of Solids 112 (2018) 291-317.
Modeling of dielectric elastomer composites
Another research thrust pertains to the mechanics of dielectric elastomers (DEs). DEs are electrically-insulating elastomeric materials, which are capable of large deformation and electrical polarization, and are used as smart transducers for converting between mechanical and electrical energy. We have developed a finite-element-based numerical simulation capability for DE composites. One potential application of this work is that of tunable phononic crystals, which are periodic materials that display phononic band gaps – frequency ranges in which elastic waves are prohibited – that may be tuned through the application of an electric field. Phononic crystals made from soft materials are capable of undergoing significant, reversible deformations so that the acoustic response of the material may be actively tuned in response to a changing environment. As a novel route to tunability, phononic crystals may be made from DEs so that their acoustic response may be tuned through electrical stimuli. Our simulation capability may be used to design electrically-tunable, soft phononic crystals, addressing both electroelastic wave propagation through a pre-deformed state and the onset of electromechanical instabilities in DE composites.
- Michael Jandron and David L. Henann. Electromechanical instabilities in periodic dielectric elastomer composites. International Journal of Solids and Structures 191 (2020) 220-242.
- Michael Jandron and David L. Henann. A numerical simulation capability for electroelastic wave propagation in dielectric elastomer composites: Application to tunable soft phononic crystals. International Journal of Solids and Structures 150 (2018) 1-21.
